В предыдущей статье было показано, что бинарные опционы никак не могут быть тотализатором. А здесь рассмотрим, могут ли бинарные опционы быть финансовыми пирамидами.
Если Вы не знаете, что такое насыщение финансовой пирамиды и чем отличаются финансовые пирамиды от многоуровневого маркетинга, то посмотрите статью про природу и суть финансовых пирамид. Там обратите внимание на то, чем отличаются друг от друга финансовые пирамиды первого и второго рода.
Самые экономически неграмотные люди называют финансовыми пирамидами всё подряд. Они считают финансовыми пирамидами и многоуровневый маркетинг, и Форекс, и фондовую биржу, и долевое строительство, и криптовалюты, и банки, и доллары, и т.д. То есть всё подряд без разбора. Ибо эти люди ни в чем не разбираются. Для них всё пирамиды, в том числе и бинарные опционы.
Здесь рассмотрим, может ли финансовая пирамида второго рода быть замаскирована под бинарные опционы. Или она легко разоблачается по поведению брокера?
Финансовая пирамида в виде бинарного опциона
На первый взгляд, кажется, что это очень интересная идея, создать финансовую пирамиду второго рода, выплаты в которой идут не всем, а только тем, кто угадал направление цены биржевого актива. Кажется, что такая пирамида должна просуществовать дольше обычной пирамиды, в которой выплаты идут каждому вкладчику.
Но, на самом деле, это очень ошибочное мнение. Ведь выплата в обычной финансовой пирамиде зависит только от размера суммы вклада участника. Но никак не зависит от его активности. Если два вкладчика одновременно вкладывают деньги в одну пирамиду, но один вкладывает в 10 раз больше другого, то он и получит в 10 раз больше. А в пирамиде второго рода, замаскированной под бинарные опционы, это правило нарушается. Вкладчик, вложивший мало денег, может заработать очень много денег благодаря своей активности. И это её слабое место.
Простая математическая модель скорости роста необходимых выплат
Для моделирования рассмотрим только один опцион. То есть, пусть у такого брокера можно делать ставки только на цену одного рыночного инструмента с одним временем экспирации. И пусть время экспирации будет единицей времени измерения всех процессов в модели. Обозначим выплату на выигрыш через α. То есть если брокер выплачивает на выигрыш, например, 75% ставки, то α=0.75. Долю выигравших вкладчиков обозначим буквой p. Суммарную долю всех депозитов, которая участвует в ставках, обозначим как ß.
Понятно, что пока идет время экспирации, пирамиде надо набрать новых вкладчиков столько, чтобы их денег хватило для выплаты по всем выигравшим ставкам. Например, если брокер выплачивает на выигрыш 80% ставки, выиграло 50% всех ставок в финансовом выражении и суммарно эти ставки составили 20% от суммарного размера всех депозитов, то нужно, чтобы во время экспирации в пирамиде прибавилось денег на 0.8*0.5*0.2=0.08 от того суммарного депозита, который там уже был.
То есть, было 100 тысяч рублей. На ставки пошло всего 20 тысяч. В выигрышных ставках задействовано 10 тысяч рублей. Брокер должен выплатить трейдерам 8 тысяч рублей. Эти деньги должны быть взяты с новых вкладчиков. Значит, пока шло время экспирации, новые вкладчики должны внести, минимум, 8 тысяч рублей.
Нетрудно сообразить, что дифференциальное уравнение, которое описывает минимально необходимые вложения, будет уравнение взрывного роста.
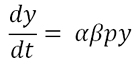
Понятно, что это нелинейное уравнение, так как, в общем случае, ß и p являются функциями времени. Считая, что это медленно меняющиеся во времени функции колебательного характера, берем их средние значения и получаем решение. Суммарный вклад в пирамиду должен расти не меньше, чем функция y=y(t).
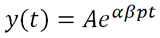
Здесь A, это начальный капитал, вложенный самыми первыми вкладчиками в нулевой момент времени. Значит, скорость наращивания вкладов должна быть не менее:
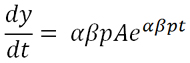
Реальное развитие всех финансовых пирамид
Из статьи по вышеприведенной ссылке, Вы знаете, что из-за конечности населения Земли (а точнее, из-за конечности скорости прироста населения), любая финансовая пирамида обречена выйти на насыщение. Этим ограничением служит даже не конечность нарастания населения Земли, а конечность нарастания людей определенной психологии в определенной стране.
Поэтому в финансовых пирамидах суммарный привлеченный капитал вкладчиков растет по такому закону, как показано на этом графике.
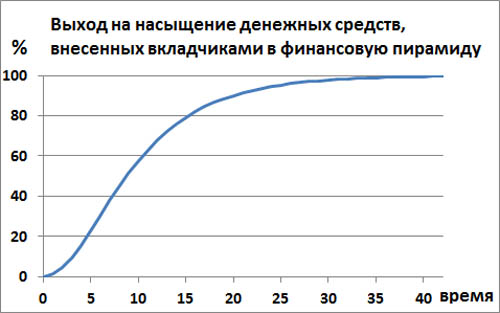
Производная этой зависимости дает скорость притока капитала в финансовую пирамиду.
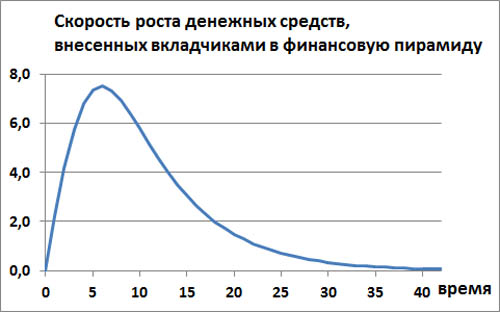
Прибыль финансовой пирамиды в виде бинарного опциона
А теперь накладывает на график скорости притока капитала график необходимой минимальной скорости наращивания вкладов, которая требуется для выплат выигрывающим вкладчикам. В результате имеем такую картину.
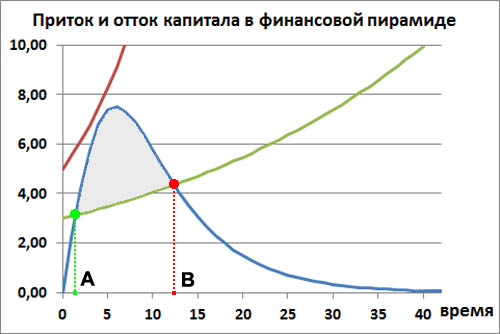
Красной линией показан пример неудавшейся финансовой пирамиды, замаскированной под бинарные опционы. Потребность в выплатах выигрышей постоянно превышают приток денег от новых участников пирамиды.
Такое происходит при достаточно больших значениях параметров α, p, ß и A.
Зеленой линией показан пример удачной финансовой пирамиды. Но сначала до точки A финансовая пирамида работает в убыток, так как выплат на выигрыши требуется больше, чем поступает денег в пирамиду. Это область, где зеленая кривая лежит выше синий кривой. Размер убытка равен площади между этими кривыми.
Затем на отрезке от A до B пирамида начинает работать в прибыль. Приходящих денег от новых трейдеров хватает на выплату всех выигрышей предыдущих трейдеров. Владелец финансовой пирамиды остается ещё и в прибыли. Его прибыль равна площади между синей и зеленой кривыми на отрезке от A до B. Эта площадь на графике заштрихована серым цветом.
Размер серой площади больше, чем размер убыточной площади между синей и зеленой кривыми от нуля до точки A. Значит, в данном примере прибыль пирамиды покроет все её убытки на первоначальном этапе до точки A. Понятно, что может быть и такой случай, когда эти площади равны или даже площадь убытков больше площади прибыли. Красная кривая соответствует случаю, когда площадь прибыли, вообще, нулевая.
Ну, а в точке B, владелец пирамиды должен срочно бежать на Багамы. После точки B убытки пирамиды начинают нарастать в геометрической прогрессии.
Поведение псевдо-брокера
Посмотрим, как должен вести себя псевдо-брокер финансовой пирамиды, замаскированной под бинарные опционы.
Из последнего графика видно, что для максимизации площади серой области нужно снизить начальную точку зеленой кривой при t=0 и нужно снизить наклон зеленой кривой. Кроме увеличения площади прибыли, это ещё приведет к тому, что уменьшится площадь начальных убытков пирамидs до точки A. А также это продлит время существования пирамиды, так как сдвинет точку B вправо.
Для достижения этих целей псевдо-брокеру нужны как можно меньше значения величин: α, p, ß и A. Но такой брокер бинарных опционов будет выглядеть очень странно и неестественно.
Снижение премии на выигрыш
Снижение параметра α для брокеров бинарных опционов не характерно. Наоборот, брокеры конкурируют между собой за то, чтобы дать трейдерам как можно больше значение этого параметра. При выборе брокера трейдеры обязательно смотрят, сколько они заработают, если их ставка выиграет.
При прочих равных условиях, трейдер выберет брокера, выплачивающего 80% на ставку, а не 70%.
"Пирамидальный" псевдо-брокер, наоборот, постарается как-то сильно много рекламировать опционы со ставками на выигрыш 60% и даже 50% и меньше. Нормальные брокеры этим не занимаются, и, в первую очередь рекламируют опционы со ставками 90% и выше.
Снижение доли выигрышей
Вы уже знаете, что занижением доли выигрышей занимаются "кухни". Если брокер уже является "кухней", то зачем ему усложнять себе жизнь и сочетать свою "кухню" с финансовой пирамидой. "Кухня" более эффективна, чем пирамида!
Снижение суммарной доли ставок
Это тоже вещь не характерная для брокеров. Обычные брокеры зарабатывают на суммарном обороте трейдеров. Поэтому брокеры не агитируют трейдеров сначала внести огромный депозит, а потом или совсем не делать ставки или делать ставки по минимуму. Наоборот, брокеры стараются агитировать трейдеров делать ставки побольше и почаще.
Для псевдо-брокера "пирамидальных" бинарных опционов со временем должно быть характерно усиление призывов как можно меньше делать ставки и делать ставки как можно меньшего размера.
Снижение суммарного начального депозита всех трейдеров
От суммарного начального депозита всех трейдеров A зависит, в какой точке зеленая кривая пересекает вертикальную ось координат на рисунке. Псевдо-брокеру с пирамидой желательно сделать это пересечение как можно ниже.
Чем это пересечение ниже, тем быстрее финансовая пирамида начнет получать прибыль и тем она дольше продержится в режиме прибыльности. Реальному брокеру, наоборот, нужно начальный суммарный депозит сделать как можно больше, чтобы быстрее выйти на точку безубыточности.
У обычных брокеров бинарных опционов никогда не встречаются какие-то ограничения на регистрацию трейдеров в только-что организованном дилинг-центре.
Заключение
Любой человек, мало-мальски, знакомый с рекламой брокеров и их курсами обучения, поймет, что брокеры бинарных опционов ведут себя совсем не так, как должны вести себя организаторы хитрой финансовой пирамиды второго рода, в которой выплаты ставятся в соответствие с некоторой активностью вкладчика. В этой статье сделано простейшее экономическое обоснование данного факта на очень простой модели.
Эту модель можно усложнить введением большого числа опционов с разными временами экспирации, выплатами на выигрыш. Модель можно усложнить и рассмотрением нелинейного дифференциального уравнения с зависимостями p=p(t) и ß=ß(t), когда "пирамидальный" псевдо-брокер начинает "подкручивать" эти параметры, чтобы сместить точку B максимально вправо уже в процессе жизни пирамиды. Но качественный анализ на графиках показывает, что это не меняет сути. Основные выводы остаются такими же, как и для упрощенной экономической модели.
Что еще можно почитать интересного про бинарные опционы:
- Почему бинарные опционы не являются рулеткой в казино? См. хорошую статью, в которой показано, чем отличаются друг от друга Прогноз биржевых цен и прогноз чисел рулетки в казино
- Что такое Математическое Ожидание на бинарных опционах. См. хорошую статью по этой теме, где заодно приводится и главная формула бинарных опционов.